Testes t: qual é o papel deles na análise de uma pesquisa?
Há diferenças estatisticamente relevantes nos seus dados?
Analisar resultados de pesquisa pode ser mais envolvente que a simples comparação de gráficos de barra.
Embora qualquer pessoa consiga ver a diferença entre dois números, entender se ela é estatisticamente relevante não é tão simples.
Digamos que você realizou uma pesquisa de satisfação do cliente para sua empresa e obteve muitos resultados para analisar. Você pergunta à sua chefe o que deve analisar primeiro, e ela diz que quer saber se homens e mulheres dão respostas diferentes. Por exemplo, homens em média dão a sua empresa um Net Promoter Score℠ (NPS) inferior ao das mulheres?
Ao analisar os dados, você vê que a avaliação média dos respondentes do sexo masculino foi 9 e a das respondentes do sexo feminino foi 12. Como você sabe se 9 é significativamente diferente de 12? É aí que entra o teste t.
O teste t é uma forma de determinar se dois números são significativamente diferentes um do outro. Existem vários tipos de teste t, inclusive o teste t online, sendo que cada um é calculado através de uma fórmula diferente.
Os três tipos mais comuns de teste t
1. Teste t de uma amostra: este teste analisa se a média de dados de um grupo (neste caso, o NPS geral) é diferente de um valor especificado.
Exemplo: a meta da sua empresa é ter um NPS significativamente maior do que o padrão do setor, que é 5. A última pesquisa da empresa atribui um NPS de valor 10. Um NPS 10 é significativamente maior do que o padrão 5 do setor?
2. Teste t de duas amostras: este teste examina se as médias de dois grupos independentes são significativamente diferentes entre si.
Por exemplo, sua hipótese é que os homens avaliam sua empresa com um NPS inferior ao das mulheres. O NPS médio dos respondentes do sexo masculino é 9 e o das respondentes do sexo feminino é 12. O número 9 é significativamente diferente de 12?
3. Teste t pareado: este teste é adequado quando você aplica a mesma pesquisa duas vezes para um grupo de pessoas. Um teste t pareado permite saber se a média mudou entre a primeira e a segunda pesquisa.
Por exemplo, você aplicou uma pesquisa ao mesmo grupo de clientes duas vezes, em abril e em maio, após terem visto um anúncio da sua empresa. O NPS da empresa mudou após clientes terem visto o anúncio?
Observe que, embora os testes t informem se algo é significativamente diferente, cabe a você determinar se a distinção é relevante. Pequenas variações podem ser estatisticamente diferentes se o tamanho da amostra for grande o suficiente.
Como fazer o teste t
Há quatro etapas para conduzir um teste t:
1. Calcular a estatística t:
cada tipo de teste t tem uma fórmula diferente para calcular a estatística t (role a página até o final para ver as três fórmulas).
2. Calcular os graus de liberdade:
graus de liberdade são o número de formas por meio das quais a média pode variar. Nesse caso, os graus de liberdade são o número de classificações NPS que você poderia ter em um determinado grupo de respondentes. Assim como a estatística t, a fórmula para graus de liberdade varia dependendo do tipo de teste t realizado.
3. Determinar o valor crítico:
o valor crítico é o limite no qual a diferença entre dois números é considerada estatisticamente relevante.
4. Comparar o valor absoluto da estatística t ao valor crítico:
se a estatística t for superior ao valor crítico, a diferença será significativa. Se sua estatística t for menor, os dois números serão indistinguíveis em termos estatísticos.
Colocando em prática
Vamos analisar o exemplo desde o início. Sua hipótese é que os homens avaliam sua empresa com um NPS inferior ao das mulheres. O NPS médio dos homens é 9, ao passo que a pontuação média para mulheres é 12. O número 9 é significativamente diferente de 12? Esse é um exemplo de quando usar o teste t de duas amostras.
1. Calcular a estatística t:
Segue abaixo a fórmula para o teste t de duas amostras, onde:
- t é a estatística t
- x1 é o NPS médio dos homens → 9
- x2 é a média das mulheres → 12
- n1 é o número de homens que responderam à pergunta do NPS → 20 homens responderam à pesquisa
- n2 é o número de mulheres → 23 mulheres responderam
- s1 é o desvio padrão do NPS dos homens → por exemplo, o desvio padrão calculado é 12,48
- s2 é o desvio padrão do NPS das mulheres → o desvio padrão calculado é 10,51
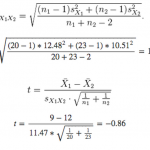
2. Calcular os graus de liberdade:
É preciso usar essa fórmula para determinar os graus de liberdade nos testes t de duas amostras. As fórmulas para outros tipos de teste são apresentadas a seguir.
3. Determinar o valor crítico:
De acordo com esta tabela, para um teste bicaudal com um nível alfa de 0,05 a 41 graus de liberdade, o valor crítico é 2,02. Observe que o teste bicaudal é usado na maioria das análises, em vez de um unicaudal, porque ele é mais conservador. Para mais informações sobre as diferenças entre testes unicaudal e bicaudal, assista a este vídeo no Khan Academy.
4. Comparar o valor absoluto da estatística t com o valor crítico:
Como o valor absoluto da estatística t é 0,86, que não é superior ao valor crítico 2,02, a conclusão é que a avaliação do NPS dos homens não é significativamente inferior à das mulheres.
Fórmulas dos outros testes t
Os testes t normalmente são realizados em uma planilha ou programa estatístico (como o Excel ou SPSS). No entanto, se você preferir fazer os cálculos manualmente, veja abaixo as fórmulas para os outros dois tipos de teste t.
Se você decidir realizar o teste t em uma planilha ou programa estatístico, como a maioria das pessoas, o processo será um pouco diferente. Em vez de comparar a estatística t ao valor crítico, a maioria dos programas calcula o valor p e o compara ao nível alfa (o nível mais usado é 0,05). Nesse caso, um valor p inferior ao seu nível alfa mostrará que os números são significativamente diferentes.
O Net Promoter Score é marca registrada da Bain & Company, Inc., da Satmetrix Systems, Inc. e de F. Reichheld.
Conheça outros recursos
Diretório de kits de ferramentas
Descubra nossos kits de ferramentas desenvolvidos para te ajudar a aproveitar feedbacks no seu cargo ou seu setor.
Crie formulários de entrevista de desligamento de colaboradores para saber onde é possível melhorar
Crie sua própria pesquisa ou formulário de entrevista de desligamento. Conheça nossas ferramentas de criação e nossos modelos prontos para começar.
Receba as autorizações de que precisa com formulários de autorização online
Receba autorizações usando um formulário personalizado de autorização. Inscreva-se gratuitamente e use modelos para criar seus próprios formulários.
Facilite o processo de solicitações com formulários online
Crie e personalize formulários de solicitações para colaboradores, clientes e mais. Comece em minutos com nossos modelos criados por especialistas.