Como analisar dados de pesquisa
Descubra como analisar dados de uma pesquisa e as práticas recomendadas para simplificar a análise de pesquisas em sua organização. Saiba como simplificar a análise de dados de pesquisas.
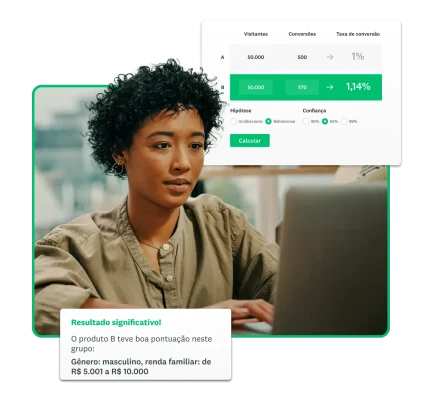
Os resultados das suas pesquisas online chegaram. Agora, você precisa analisar os dados para entender os resultados e apresentá-los de forma simples de entender e aplicar.
Neste guia, você descobrirá o que é análise de pesquisas, os diferentes tipos de dados com os quais pode interagir e seis etapas para fazer uma análise de dados de pesquisas eficaz.
O que é análise de pesquisas?
Análise de pesquisas é o processo de transformação de dados de pesquisas em resultados e insights práticos. Com base nas informações obtidas na pesquisa, essa análise ajuda a transformar dados brutos em resultados práticos.
Para simplificar a obtenção de insights valiosos dos dados na análise de pesquisas, trace um plano. Ao entender o que deseja alcançar, você consegue analisar os dados de maneira mais eficaz.
Para obter mais informações e orientações detalhadas sobre como criar e analisar pesquisas, assista ao nosso webinar.
Os diferentes tipos de dados de pesquisa
Os tipos de pergunta usados na pesquisa determinam os tipos de dados que você recebe, que podem ser quantitativos ou qualitativos.
Dados quantitativos são informações numéricas. Por exemplo, na pesquisa do Net Promoter Score® (NPS), as pessoas respondem usando uma escala de 1 a 10. Portanto, todas as informações obtidas são numéricas, gerando dados quantitativos que podem ser usados para comparações diretas e análises estatísticas.
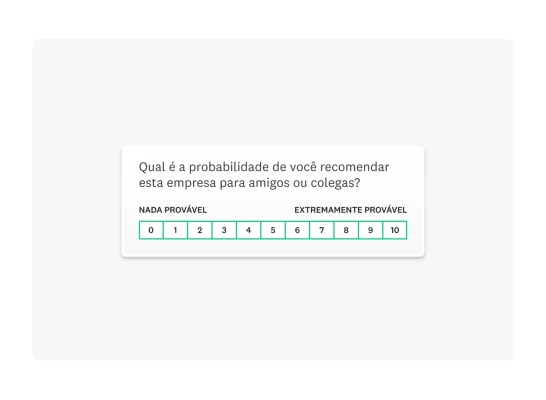
Já os dados qualitativos se baseiam em informações não numéricas. Esse tipo de pesquisa visa descobrir o “porquê” por trás de dados numéricos. Por exemplo, você pode perguntar aos respondentes por que escolheram determinado número, oferecendo espaço para explicarem sua resposta. Embora seja mais difícil analisar dados qualitativos, é fundamental descobrir a história por trás dos dados.
Dados numéricos são fantásticos para monitorar o progresso com o tempo. No entanto, se você quer entender a motivação por trás das respostas, o ideal é usar uma pergunta complementar para gerar dados qualitativos.
Como analisar dados de uma pesquisa em 6 etapas
Descubra como você pode entender os números e o significado por trás dos seus resultados.
Limpe seus dados
Antes de começar a análise da sua pesquisa, certifique-se de que seus dados sejam úteis. Limpar os dados da pesquisa significa decidir quais respondentes excluir da análise, removendo respostas duplicadas e de baixa qualidade.
É possível que algumas pessoas tenham respondido somente a algumas perguntas e outras tenham respondido à pesquisa de forma apressada e sem atenção. Esses casos podem influenciar na baixa qualidade dos dados, afetando a precisão dos seus resultados.
A análise da qualidade das respostas ajuda a identificar respostas que não atendem aos critérios da sua pesquisa. Por exemplo, se você estiver coletando dados relacionados ao sentimento de clientes, a resposta de alguém que não seja cliente não é útil.
Prepare os dados da pesquisa facilitando sua leitura, homogeneizando a formatação e classificando-os de forma lógica para ter um conjunto de dados limpos e claros para a análise.
Comece com as perguntas mais importantes
As perguntas mais importantes são aquelas que conduzirão toda a pesquisa. Elas estão relacionadas aos objetivos da pesquisa.
Comece com a pergunta mais importante da pesquisa antes de se aprofundar nos detalhes granulares dos dados. Por exemplo, a tabela de resultados abaixo é o ponto de partida de uma pesquisa com a pergunta “Você compraria esse novo produto se ele estivesse disponível hoje?”.
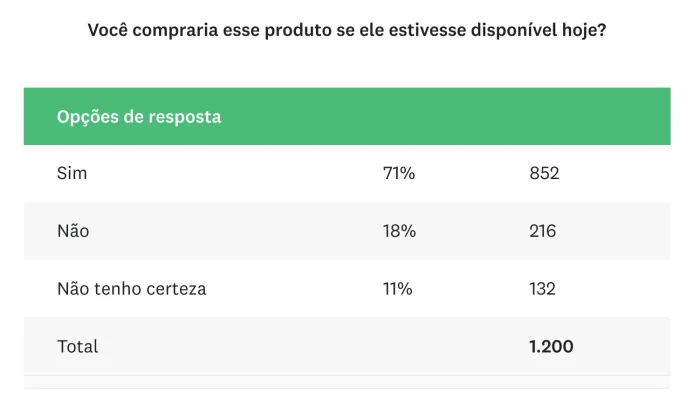
A grande maioria das pessoas respondeu de maneira positiva. Portanto, você pode continuar com dados de outras perguntas para obter mais informações sobre esse produto.
Perguntas mais abrangentes ajudam a identificar as principais opiniões e ideias. Após estabelecer essa base, você pode seguir para as partes mais complexas da análise de dados para responder às perguntas da sua pesquisa.
Segmente seus dados
Uma das melhores formas de entender melhor os dados é segmentá-los. Você pode usar a tabulação cruzada para dividir seus dados em grupos menores baseados em características semelhantes. Por exemplo, você pode filtrar os dados por respostas de pessoas que tenham um histórico específico. É possível filtrar, comparar e criar regras para analisar os dados em cada segmento de usuário.
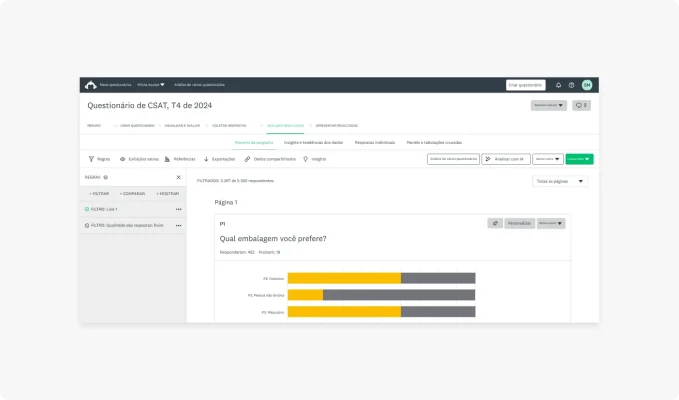
Os filtros são uma maneira poderosa de obter insights abrangentes dos dados. Por exemplo, se você quiser descobrir o desempenho de um produto em diferentes grupos, inclua perguntas de perfil demográfico na pesquisa. Com uma pergunta de faixa etária, é possível filtrar instantaneamente as respostas de acordo com a idade. A comparação desses conjuntos de dados pode revelar em que nível cada faixa etária gosta do seu produto, ajudando a identificar instantaneamente discrepâncias ou perfis demográficos mais insatisfeitos.
É possível filtrar por:
- Gênero;
- Área de trabalho;
- Idade;
- outros fatores de perfil demográfico; e
- outros fatores psicográficos.
Embora dados qualitativos não gerem porcentagens ou números brutos que você possa usar aqui, é possível recorrer a ferramentas de análise de texto. Ao coletar respostas escritas e avaliá-las usando uma dessas ferramentas, é possível gerar uma análise de sentimento das pessoas respondentes.
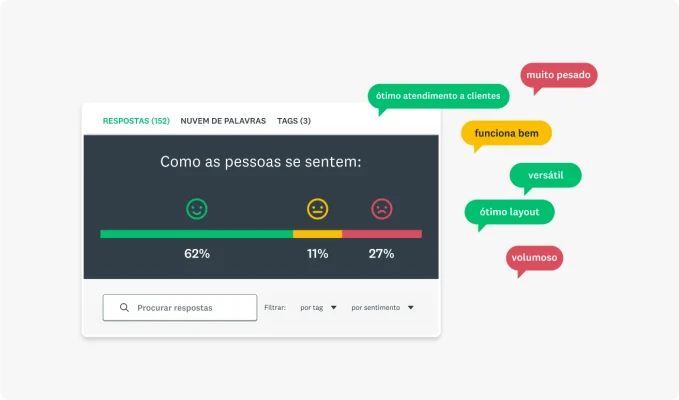
Faça uma análise estatística e contextual
Para converter dados brutos em insights, é preciso ter relevância estatística. É preciso garantir que os dados revelem uma descoberta, não escolher casos a dedo. A análise estatística revela se as tendências observadas são relevantes e o que os dados sugerem quando combinados a outros conjuntos de dados.
É possível comprovar a relevância estatística de diferentes maneiras:
- distribuições de frequência;
- teste t;
- teste de análise de variância;
- análise de tabulação cruzada;
- análise de agrupamento; e
- análise de fatores.
Além da análise bruta, outros fatores determinam a relevância dos resultados. Por exemplo, a comparação do número total de respostas e da taxa de conclusão com o tamanho total da amostra revela se os resultados representam um grupo estatisticamente relevante.
Da mesma forma, é uma boa ideia considerar a margem de erro nos resultados da pesquisa. Ela indica o quanto os resultados refletem a população como um todo. Uma margem de erro pequena sugere uma alta confiança na precisão dos resultados. Uma margem de erro grande sugere que os resultados podem não representar a população como um todo.
Você precisa de mais respostas para ter um nível de autoridade maior nos resultados? O SurveyMonkey Audience pode ajudar você.
Compare e monitore seus resultados
A comparação com referências é o processo de comparação de resultados com médias de outras empresas ou do setor. Também é possível comparar seus resultados com outros resultados seus por meio da repetição de pesquisas coletando dados em diferentes períodos, como trimestres ou anos.
Empresas do mundo todo usam a comparação de experiência de clientes para descobrir a opinião de clientes com relação à concorrência.
A análise longitudinal permite descobrir a mudança dos resultados de pesquisas com o tempo. Por exemplo, se você organiza um congresso anual, pode pedir para as pessoas participantes avaliar sua satisfação com o evento usando uma pesquisa de feedback de congresso. Se a taxa média de satisfação diminui com o tempo, você tem um ponto inicial interessante para pesquisas futuras.
Você pode combinar a pergunta de satisfação a uma pergunta aberta pedindo para as pessoas explicarem sua escolha. Esses dados qualitativos esclarecerão o que pode estar causando a queda de satisfação, ajudando você a tomar medidas práticas para resolver o problema.
É possível até mesmo monitorar dados de diferentes subgrupos. Vamos supor, por exemplo, que as taxas de satisfação vêm aumentando anualmente para a equipe de marketing, mas não para a administração. Pode ser interessante analisar as respostas da equipe de administração a várias perguntas para tentar entender por que ela está menos satisfeita que os demais participantes.

Crie e compartilhe um relatório convincente
Os dados da sua pesquisa têm o poder de contar uma história. Comece com a pergunta mais importante, descreva suas descobertas e continue a partir daí. O que você quer descobrir? O que você descobriu com seus dados? Quais descobertas específicas se destacam ou são particularmente interessantes?
Sempre que possível, use recursos visuais em seu relatório. É entediante analisar diversos parágrafos de explicações de números. Um gráfico simples ou uma nuvem de palavras resume os resultados e permite que as pessoas entendam a mensagem dos dados de maneira intuitiva.
Agora que você analisou seus dados e comprovou a relevância estatística, chegou a hora de mostrá-los ao mundo. A criação de um ótimo relatório é a última etapa da análise prática da pesquisa. Ele permite compartilhar as descobertas com colegas, que podem inspirar mudanças na sua organização.
Leitura relacionada: como usar 6 gráficos básicos para criar relatórios eficazes
Os erros mais comuns na análise de pesquisas
Há várias armadilhas comuns na análise de pesquisas. Confira alguns erros a serem evitados.
Confundir correlação com causalidade
O erro mais comum que as pessoas cometem ao analisar pesquisas é confundir correlação com causalidade. Causalidade é quando um fator é a causa direta de outro. Correlação é quando dois fatores se movem juntos, mas não estão relacionados.
Um ótimo exemplo são os efeitos do tempo frio. Por exemplo, beber chocolate quente e usar luvas são duas variáveis correlacionadas, pois tendem a variar juntas e no mesmo sentido. Porém, uma não causa a outra. As duas são provocadas por um terceiro fator, o frio.
O simples fato de dois fatores serem paralelos não significa que eles sejam relacionados. A análise de correlação ajuda a identificar a relação entre seus dados.
Ao confundir correlação com causalidade, você conecta dois dados a um motivo terciário.
Escolher os dados de forma criteriosa
Os resultados da sua pesquisa contam uma história. No entanto, ao escolher os dados de forma muito criteriosa, ou seja, ao escolher os principais dados que validam sua hipótese, você pode perder a visão geral.
Ao tentar provar algo com uma pesquisa, pode ser frustrante quando os dados não batem. Os clientes podem não concordar com uma afirmação importante ou os dados podem não ter relevância estatística. Independentemente da sua descoberta, você não pode selecionar os dados a serem usados de forma extremamente criteriosa.
Se escolher quais dados usar nos cálculos, você influenciará na precisão dos resultados da pesquisa.
Calcular os resultados de forma apressada
A SurveyMonkey sabe, melhor do que ninguém, que fazer pesquisas e coletar resultados pode ser extremamente empolgante. No entanto, ao calcular os resultados de forma apressada, você pode deixar passar dados importantes ainda não fornecidos.
Para ter um alto nível de confiança nos dados, é preciso ter grandes conjuntos de respostas. Ao calcular os resultados antes do tempo, você arrisca ter menos respostas do que o necessário para alcançar relevância estatística.
Imagine que os resultados da sua pesquisa mostrem que 100% dos clientes têm interesse no novo recurso de um produto. Embora esse número pareça incrível, se apenas uma pessoa respondeu à pesquisa, qual é o nível de confiança de que as respostas realmente refletem sua base geral de clientes?
Dicas para melhorar a qualidade dos dados de pesquisas
Os tipos de pergunta usados na pesquisa determinam os tipos de dados que você recebe e a qualidade deles. A qualidade dos dados da pesquisa refletem a qualidade das perguntas.
Confira algumas dicas:
- Colabore com colegas de trabalho: compartilhe sua pesquisa com colegas antes de publicá-la para descobrir quaisquer problemas que ela possa ter. Podemos deixar passar problemas simples no estilo das perguntas. Colabore com outras pessoas para criar pesquisas abrangentes, equilibradas e eficazes.
- Use diferentes estilos de pergunta: o uso de perguntas abertas e fechadas torna a pesquisa mais equilibrada. O uso de perguntas neutras, simples, diversificadas e fáceis de entender ajuda a obter dados de alta qualidade.
- Aproveite as integrações: ao integrar outros aplicativos, como sua plataforma de CRM, você automatiza a integração de dados de pesquisas a outras áreas dos seus negócios. Você pode facilitar ainda mais a análise de dados ao trabalhar com outras ferramentas, ajudando a simplificar a identificação de insights úteis.
- Use pesquisas de especialistas: como a qualidade das perguntas afeta os dados, você pode recorrer aos modelos de pesquisas criados por especialistas para garantir resultados melhores. Os modelos ajudam a aumentar a probabilidade de obter dados confiáveis.
Ao melhorar a qualidade das suas pesquisas, você naturalmente começa a coletar dados de melhor qualidade.
Pesquisas simples com a SurveyMonkey
A análise de dados de pesquisas envolve diversos aspectos, desde entender os principais resultados até segmentar os dados e gerar relatórios.
A SurveyMonkey tem ferramentas de análise de pesquisas e modelos que facilitam a coleta de respostas confiáveis e o alcance do seu público-alvo.
Inscreva-se para usar ferramentas e modelos criados por especialistas.
Perguntas frequentes
- O que é análise de regressão?
- O que é análise longitudinal?
- Como determinar o tamanho da amostra?